Constrained Sessile Drop
The Constrained Sessile Drop is a method for optical measurement of surface tension based on the contour curvature of a perfectly symmetrical sessile drop.
Why can surface tension be measured from the shape of a sessile drop?
The surface tension counteracts the increase of a surface. Therefore, a drop in zero gravity would be spherical, because a sphere has the smallest surface area per unit volume.
A sessile drop under the influence of gravity has a flattened shape due to its own weight. The deviation from the shape of a sphere or spherical cap is greater the larger the weight and the lower the surface tension. If the dimensions and density of the drop are known, the surface tension can be calculated on the basis of the Young-Laplace equation (see below for explanation) using optical drop shape analysis.
What does "constrained" mean in the context of the sessile drop?
The drop is “constrained” because it is forced into a certain shape. For the measurement of surface tension on the basis of the drop contour, a drop that is as high as possible and at the same time absolutely symmetrical is required. A drop dosed onto an arbitrary surface will no longer grow in height above a certain volume and will form an increasingly irregular shape. It will therefore give inaccurate results, especially for liquids with low surface tension.
For the Constrained Sessile Drop method, the drop is dispensed onto an exactly circular sample platform with sharply cut outer edges. The edges form a wetting barrier so that the drop becomes higher as the dispensing volume increases and takes on a symmetrical shape instead of stepping over the edges of the pedestal. For such a drop, the surface tension can be determined very accurately.

There are already optical methods for measuring surface tension – why do we need another one?
In fact, surface tension has long been measured using a pendant drop, a drop suspended from a dosing needle. In some cases, however, the Constrained Sessile Drop offers advantages. For example, in advance of a contact angle measurement, the necessary purity of the test liquids can be checked using the surface tension without having to change the dosing needle or, in the case of pressurized dosing units such as the Liquid Needle, without having to change the test setup. Liquids with low surface tension can also be analyzed with a larger dosing volume, where a pendant drop would fall from the needle.
Another advantage is easier analyses of molten solids. Samples can be melted directly on the sample platform, which simplifies preparation and cleaning and facilitates measurements and thermally isolated conditions.
What is the theoretical background for the Constrained Sessile Drop method?
The interfacial tension σ between the inner and outer phases (i.e. the surface tension between the air and the drop) results in an increased pressure inside the drop. The relationship between the pressure difference Δp, the principal radii of curvature of the surface r1 and r2 and the interfacial tension is described by the Young-Laplace equation:

Under the influence of gravity, the drop is deformed because hydrostatic pressure is generated inside the drop due to the weight force, which influences the radii of curvature r1 and r2. Since the hydrostatic pressure is height-dependent, the curvature of the drop interface also changes in the vertical direction. The following figure illustrates this fact on the basis of a pendant drop.
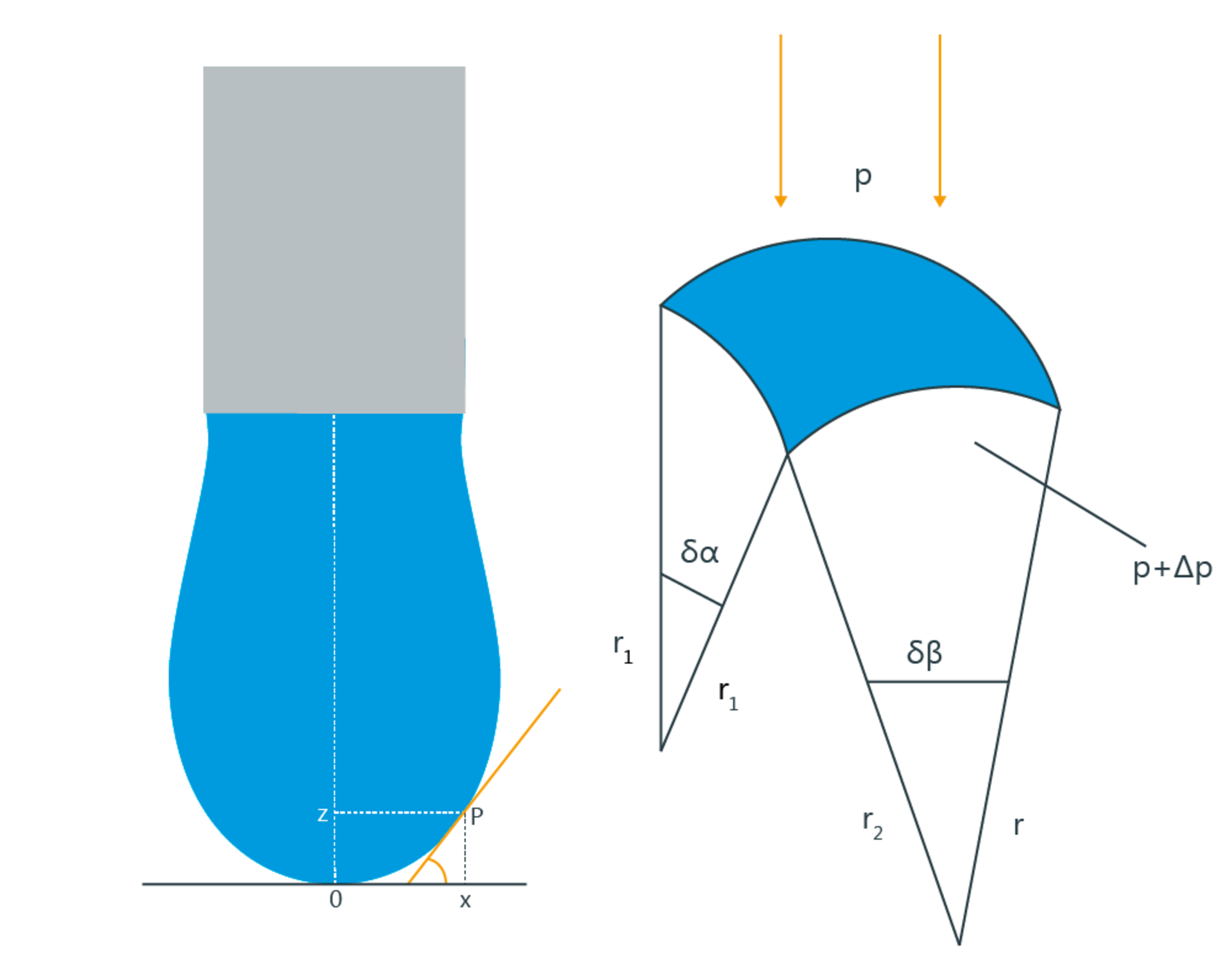
During a measurement, the image scale of the video image is first captured to make the real drop dimensions accessible. The drop contour is then determined from the video image of the dosed drop. A numerical procedure is then used to vary a shape parameter, denoted B, until the calculated drop contour matches the actual one. The surface tension is calculated from the density difference Δρ between air and drop liquid and the adjusted B parameter.
Literature
Laura M. Y. Yu; James J. Lu; Yawen W. Chan; Amy Ng; Ling Zhang; Mina Hoorfar; Zdenka Policova; Karina Grundke; A. Wilhelm Neumann, Constrained sessile drop as a new configuration to measure low surface tension in lung surfactant systems. In: J Appl Physiol 97 (2004), P. 704-715.







