表面自由能(SFE),表面能。
表面自由能(SFE)是增加固相表面积所需的功。 SFE对液体对固体的润湿性具有决定性的影响。 因此,对于优化涂覆工艺以及对于任何其他类型的固液接触而言,它都是重要的参数。
什么时候是SFE,什么时候是表面张力?
表面自由能(SFE)和表面张力(SFT)在物理上是等价的。SFE通常用于固体表面,SFT用于液体表面。然而,偶尔也会提到固体的表面张力。
SFE以单位mJ/m²(毫焦耳/平方米)作为单位面积的能量,据此,SFT常用的等效单位mN/m(毫牛顿/米)也经常被使用。公式符号为σ(small sigma),更少见的是γ(small gamma)。
"自由 "一词表明,这部分能量是可以转化为机械功的,与内能不同的是,内能还包含与热有关的熵。在实际应用中,"自由 "一词往往被省略。
SFE与润湿性之间有什么联系?
每一个系统都力求获得尽可能低的自由能状态。因此,液体在给定的体积下,由于SFT的作用,表面积最小;在失重状态下,它们会形成球形液滴。然而,固体不能通过变形使其表面最小化,但它们可以与液体形成界面以降低自由能,即可以被润湿。因此,固体的SFE与它的润湿性密切相关。
如何影响SFE?
例如,在粘接、涂层或印刷时,需要良好的润湿性和相应较高的SFE。在其他领域,如腐蚀和防潮,必须降低润湿性。大量的技术工艺需要为固体表面与液体接触做制备工作--其中大部分直接或间接地改变了SFE。
提高SFE对于塑料表面来说是至关重要的。典型的方法是等离子、火焰和电晕处理,以及使用氧化剂的化学工艺。工业清洗可以通过去除脂肪或油类低自由能污染,使表面获得更高的SFE。
低SFE和相应的低润湿性通常是通过涂上低自由能物质来实现的。例如涂有PTFE的炊具或使用油类进行防腐。
SFE和接触角有什么关系?
用接触角的方法来测量润湿性,即通过光学法测定液滴轮廓盒固体表面(基线)的夹角润湿性的测量是接触角(CA)θ(small theta),通常通过光学方法确定为液滴轮廓与表面平面(=基线)的夹角。根据杨氏方程,CA是基于热力学平衡下的三相体系,每一个分量都力求使表面或界面最小化:
杨氏方程定义了这些分量之间有如下关系:



计算SFE的模型不同,这些模型的主要区别在于对界面相互作用的阐述和计算。 最常见的是极性部分和非极性部分相互作用的细分,其中SFE和SFT分为极性和非极性。简化后假设极性和极性部分发生相互作用,非极性和非极性部分相互作用。
为了确定SFE,需用至少两种液体测量接触角,其中SFT及其极性和非极性值均已知。 为了计算SFE,将杨氏方程与该方程组合以计算相互作用。
SFE的极性和非极性部分是什么?
相对较强的极性相互作用是由分子中电子密度的永久性和局部不对称造成的。在液体中,最典型的例子是水,水的极性是导致高SFT的原因,固体表面极性高的典型例子是玻璃。
非极性部分的相互作用通常较弱,它们是由于分子中电子密度分布的统计波动,造成不同位置的暂时性电荷差异形成的,这就导致了分子间的静电吸引。烷烃和一些塑料如聚乙烯或聚丙烯专门形成非极性相互作用,这也是许多塑料和水润湿性差的原因。
上述预处理方法实质上是增加了SFE的极性部分,因此使塑料的表面张力更接近水的表面张力。 根据两组分模型,如果固体的SFE和液体的SFT一致,且各个极性和非极性部分也一致,则润湿性和附着力最大。
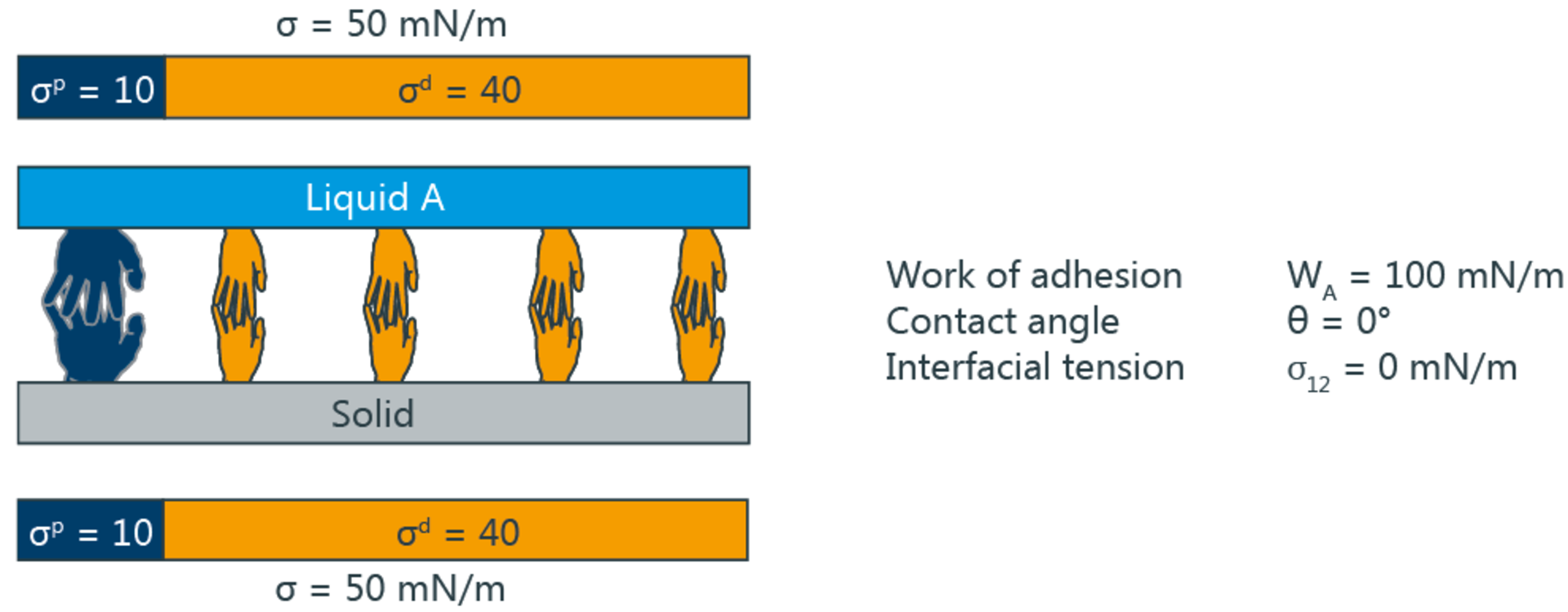
下图显示了用液体和固体极性和非极性部分相互作用的方法,来预判液体在固体表面的润湿性和附着力。大手象征着极性,小手象征着非极性。在上图中,极性和极性,非极性和非极性可以完全相互作用在一起,从而产生最大的附着力和0°的接触角。下图是交互分量不相同的例子。

SFE不能用达因笔来测定吗?
达因笔仍用于检查表面的润湿性。 用户和某些达因笔制造商将结果解释为SFE。 该方法看似显而易见:将几种SFT下降的液体混合物一个接一个地施加到表面上。 形成非流动膜,即完全润湿表面的第一液体的SFT等于固体的SFE。
但是,他们没有考虑液体和固体间极性和非极性相互作用的性质。 结果,达因笔测试的结果不能转移到与大多数其他液体接触。 因此,在技术过程中,固体的行为通常与达因笔测试后所预期的完全不同。
下面的例子可以说明这一点。极性水比非极性的二碘甲烷(DIM)具有更高的SFT,按照达因笔的理论,表面张力越低,在固体表面的润湿性应该越好。在非极性塑料上,水的接触角比DIM高得多。但在高极性的玻璃表面,则情况完全相反。水的表面张力比二碘甲烷高,但水的接触角比DIM的接触角小得多。这个例子说明,单凭液体的SFT量不足以建立润湿和SFE之间的关系。已发表的科学研究报告《为什么测试油墨不能说出固体表面自由能的全部真相》对油墨测试方法进行了全面的讨论(见文献列表)。
参考文献
- F. M. Fowkes, Attractive Forces at Interfaces. In: Industrial and Engineering Chemistry 56,12 (1964), P. 40-52.
- M. Jin, F. Thomsen, T. Skrivanek and T. Willers, Why Test Inks Cannot Tell the Whole Truth About Surface Free Energy of Solids. In: K. L. Mittal (Ed.), Advances in Contact Angle, Wettability and Adhesion Volume 2 , Hoboken, New Jersey and Salem, Massachusetts 2015, P. 419-438.
- D. H. Kaelble, Dispersion-Polar Surface Tension Properties of Organic Solids. In: J. Adhesion 2 (1970), P. 66-81.
- D. Owens; R. Wendt, Estimation of the Surface Free Energy of Polymers. In: J. Appl. Polym. Sci 13 (1969), P. 1741-1747.
- W. Rabel, Einige Aspekte der Benetzungstheorie und ihre Anwendung auf die Untersuchung und Veränderung der Oberflächeneigenschaften von Polymeren. In: Farbe und Lack 77,10 (1971), P. 997-1005.
- T. Young, An Essay on the Cohesion of Fluids. Philosophical Transactions of the Royal Society of London, The Royal Society, London 1805, Vol. 95, P. 65-87.






